前段时间在 小石 同学的安利下玩了一款叫HyperRogue的游戏，这是一个在双曲平面上的roguelike，著名的一个非欧几何——罗巴切夫斯基几何。于是想介绍一下罗氏几何，与推荐一下这款游戏，能更直观的体验非欧几何的魅力。 本文主要数学内容来自【俄】诺尔金的《罗巴切夫斯基几何学初步》¹。

• 欧几里得几何学
  • V. 平行公理
• 罗氏几何的简要推论
  • 平行线的定义
  • 罗氏几何里的直线关系
• HyperRogue游戏的简单玩法介绍
• 模型与曲线
  • 笛卡尔盘模型
  • 其他模型
  • 曲率半径
  • 有着重要地位的曲线——圆、等距圆与极限圆
• 罗氏几何与欧氏几何的相容性，以及其后世影响

#欧几里得几何学

几何学起源于遥远的远古时代，大约在公元前七百年从古埃及传入古希腊后，几何也开始发展成为一门科学。最为重要的是，在那里，演绎推理与公理法被应用到了几何上，最著名的就是公元前4,3世纪的欧几里得（Euclid）所著的《几何原本》，至今仍是优秀的推荐大家去看一看的书籍。 公理体系的本身是由不加定义的概念与不加证明的公理开始的。为了解它们的必要性，几何学中的定义可举例如下：由同一点出发的两条射线所构成的图形称为角。但是为了定义角的概念，用到了点，和自该点出发的射线的概念。我们是不是也要给点和射线下定义呢？我们确实能找到这样的定义：自已知点出发的射线，是指所有在通过已知点的直线上，并且位于该已知点的一侧的点的集合。但是，这个定义中又有新的概念，“通过点的直线”和“位于一侧”。显然这样的方法不可能无限进行下去，所以我们必须给定一些没有定义的概念作为体系的基础。在几何学里，留下的基本概念是“点”“直线”“平面”“属于”“介于”“合同”。 公理的地位也是如此。在所有能确定正确与否的句子中（我们称之为命题），想推出某一个是正确的，必须依赖另外的命题。从命题里选出几个最基本的作为默认正确的公理，并以其作为推理的基础。公理的正确性的问题是无法在公理体系内解决的，但这并不等于说这些问题是解决不了的。几何的基本概念是抽象的，但是在生产实践中，我们可以将其赋予到实体上。比如，在最简单的测量实践中，我们将直线解释为拉紧的绳子；在力学上解释为物体依惯性运动的轨道，在光学和天文学上解释为光的射线。同样的可以解释其他的基本概念，并验证它的公理的正确性，从而断定，由公理经过逻辑推理得出的定理都是正确的并被生产实践所使用。因此，几何公理与定理的正确性是在几千年的时期里被人类的实践活动和科学工作不断的证实的。

欧几里得在几何原本中的公设体系并不是那么的精细，18世纪的著名数学家希尔伯特（Hilbert）的《几何基础》系统性的总结提出了这一套公理。但是除了一条公理——平行公理——以外，其余的并不是我们的重点，有兴趣的读者可以点开黑幕信息查看。

#V. 平行公理

公理是整个几何公理体系的基石，自然人们就希望，作为“不用证明”的公理，形式越简单，看起来越显然，就越可以作为正确的基础。人们特别注意到欧几里得的《几何原本》中的所谓“第五公设”²，欧几里得是这样表述的：

如果一直线和两直线相交，所构成的两个同侧内角之和小于两直角，则这两条直线延长后必在这一侧相交。

它和几何原本中的其他公理相比，甚至比很多定理来讲，都要复杂很多。所以当时很多人都认为，这个命题不应该是公理，应该是能够被证明的。追求它的证明的工作持续了几千年之久，许多不同的人提出了许多不同的证明。但是仔细研究会发现，这些证明时大都或明显地或隐蔽地引入了新的公理。诸如：“两条不相交的直线其间的距离不会无限增大”，“对于任何图形常有任意大小的相似图形存在”，“三角形的内角和等于两直角”，“通过一角内任意一点，可以引直线与这角的两边分别相交”，等等等等。我们这里采取如下的在现在的课本里常见的叙述：

V. （平行公理）通过直线外一点，在平面上能且只能做一条直线，与已知直线不相交。

但是，没有一个人能够真正使用欧几里得的其他公理证明平行公理。匈牙利的集合学家B·波里埃给他的儿子约翰写道：

“希望你不要专意克服平行线的理论了；你会在这上面花费掉所有的时间，而终生不能证明这个命题……这个昏无天日的黑暗将使成千个像牛顿那样的天才全被吞没。它任何时候也不会在地上明朗化，并且不让不幸的人类，即使在几何学上得到任何成功。这是永远留藏在我内心里的巨创。”³

驱散这个黑暗的就是罗巴切夫斯基（Lobachevsky）。他同样在试图证明第五公设时发现了这个问题。他转而试图采取第五公设的相反命题作为公理，如果发现了这样改变后的公理系统有矛盾，也就证明了第五公设。但是从这个公理系统得出的推论，一个比一个奇特，它们似乎都和我们习惯的观念相冲突，但是仔细分析后却发现在逻辑上没有任何的矛盾。也就是，他创立了一个新的几何：罗巴切夫斯基几何，在现代也常被称作双曲几何。

#罗氏几何的简要推论

#平行线的定义

如果采取上面的平行公理，得到的几何学体系就是我们在课本中都能够见到的欧几里得几何，也就是我们通常说的两条不相交的直线即定义为平行。但是我们希望使用的是另一条第五公设的相反命题⁴：

通过直线外一点，在平面上至少能做两条直线，与已知直线不相交。

如图，考虑直线C'C和直线外一点A，从A做垂线AB（线段AB称为A对于直线CC'的指针），在AB的右侧考虑所有从A出发的射线。有些射线和BC相交（如AD，AE），有些和它不相交（如AS），从AB开始逆时针旋转，找到第一条和BC不相交的射线比如AP，我们称之为射线AP与BC平行（一定有这样的一条直线的证明略）。同样，左侧也能找到一样的一条平行射线AP'。自然会有一个问题，这两个射线是不是属于同一条直线。如果认为属于同一条直线，就相当于认为角BAP是直角（角BAP称为点A对于直线CC'的平行角），就回到了欧几里得的平行公理，这是我们不希望的。也就是说，在罗氏几何里，这两条射线所在的直线之间，还会有别的直线，它们与已知直线既不平行也不相交，我们称为超平行，比如图里的AR。

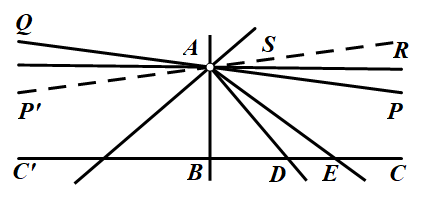
#罗氏几何里的直线关系

可以证明这样的定理，平行角随着指针的递增而递减，并且任意的锐角，都可以找到一个指针使得该角作为其平行角。这个图可以让我们先对罗氏几何有一个初步的感受，这里就开始和我们常见的欧几里得几何有一些不同了：

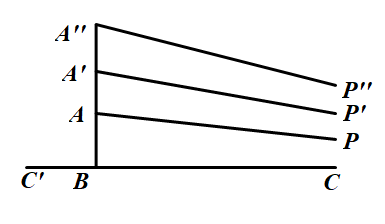
在A点上移的过程，A点右端与CC'平行的射线上移的慢。我们再进一步向前推，给定一条已知直线，和一条与已知直线不平行也不垂直的斜线，一定能找到已知直线的一条垂线，使它与斜线平行：实际上就是上图，从A''P''开始，保持直线平行并向下移动，总可以移动到BC这样一条垂线。事实上，对于任何的角，都可以在角内部做出一条与角的两条边都平行的直线。方法是：做角平分线，然后在角平分线上找一条垂线使其与角的边平行。

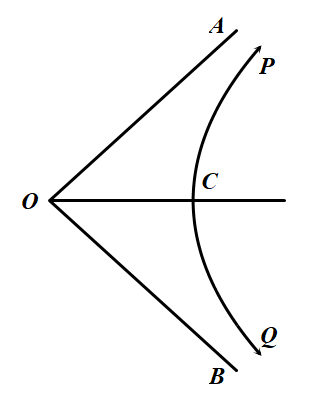
我们甚至可以做出一组由直线组成的图形，叫做退化多边形，其中的直线两两平行：

可以理解为多边形在其中的点趋于无穷远下的极限。平行之外，还有超平行。最简单的做出超平行直线的方法就是在上一节的第一张图里，过A做出指针AB的垂线，也就是垂直于直线AB的两条直线超平行。相反，超平行的两条直线也可做且仅可做一条公垂线。

我们看到，已经有些直线在画图的时候被扭曲成了曲线的形状。这也是没有办法的，毕竟我们所在的空间不是罗氏空间嘛。那么，想更好的表示罗氏几何的性质，最好的办法就是将其一一对应到欧几里得平面上的物体，也就是下下一章的模型。

#HyperRogue游戏的简单玩法介绍

想了想，好像没有很好的位置介绍游戏的基本玩法了，就放在这里好了。HyperRogue顾名思义，是一个Roguelike游戏。游戏大致是回合制，玩家动一步怪物动一步，主要目标是收集宝石也就是分数。游戏有很多种大陆，每一个大陆都有一个独特的机制，比如像扫雷一样的Minefield，吃到镜子碎片可以产生分身的Hall of mirrors，带领不同颜色的虫子相互战争的Hive等等。每个大陆也有自己的宝石类型，收集的宝石越多这个大陆的怪物也会刷出的越多。在收集到30个以及60个宝石后会解锁一些大陆，有的大陆还有自己特殊的要求，比如地狱需要9个不同的大陆每个大陆至少10个宝石。这里可以看到一个简单的简介。

游戏很大程度上基于这样一个（同样行文里没有很好的位置叙述的）事实：罗氏几何里的圆的面积几乎是半径的指数函数。对比欧几里得几何，也就是我们日常生活的几何，它的圆的面积只是半径的平方。也就是说，这个大陆比我们日常生活的几何，大得多得多。比如说，这个Ivory land，实际上占了整个无限大的上半平面：

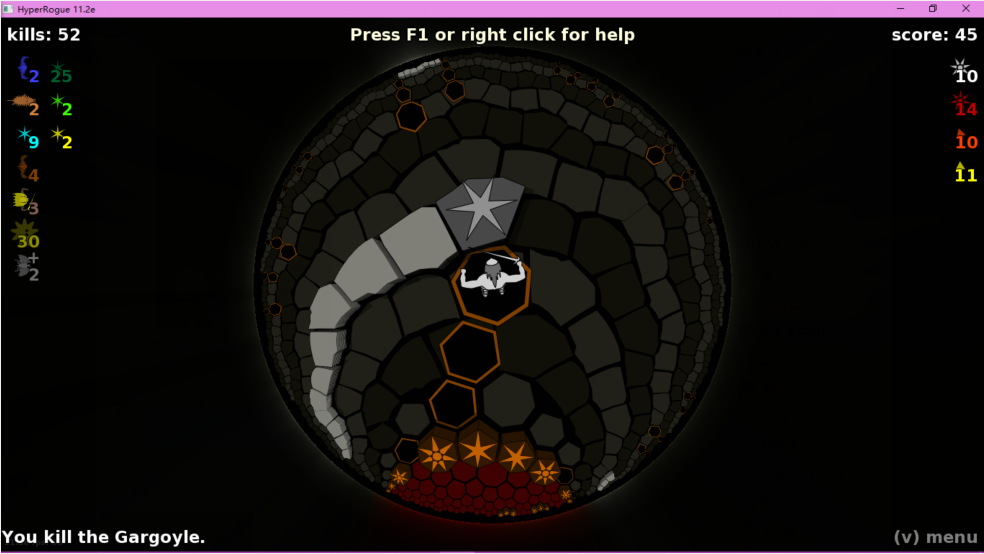
如果在欧几里得几何里，一个平面被占掉一半之后，就只有一个半平面了（是一个/半平面，不是一个半/平面！），顶多能再划分出一条有限宽的带。但是罗氏几何不一样。上面说过的那个退化多边形就是一个例子。用直线分掉一个半平面之后，还有很多很多的半平面。这也说明了这个游戏无限的可能性（笑）

#模型与曲线

所谓罗氏几何的模型，就是在欧几里得几何里表现出罗氏几何的点线等元素，但是并不一定仍然保持是直线，或者并不一定保持角度的大小不变，因为扭曲是一定存在的。最常见的模型，也是HyperRogue里使用的模型，就是笛卡尔盘模型（Poincare disk model）。

#笛卡尔盘模型

笛卡尔盘模型以欧几里得平面上的一个圆为基础，将圆的内部的点等价到罗氏几何的点。注意只有圆的内部的点才有意义，圆的边界上的点被认为是无穷远处的理想点。双曲直线（涉及不同几何的交叉的时候，以后会将罗氏几何里的直线称为双曲直线，将罗氏几何的平面称为双曲平面）则被对应到大圆的直径或与大圆正交的小圆（所谓正交，就是两圆在交点处的切线相互垂直）。平行的双曲直线表示为相交于大圆上点的两圆/直线，而超平行的则是不相交的。如图，abc都是双曲直线，b与c平行，与a超平行，a与c相交。读者可以尝试验证一下上面的公理与每条定理的正确性。

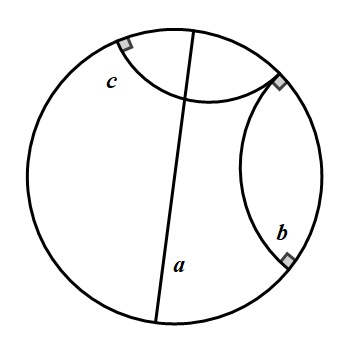
双曲直线的垂直仍然是两圆/直线在交点处垂直。事实上，笛卡尔盘模型是保角的，也就是它保持原罗氏几何里的角度不被扭曲，我们看到的图景至少在近处仍是接近真实的。

#其他模型

当然还有其他的很多模型。Klein的圆盘模型不是保角的，形状会被扭曲，但是它将直线对应到直线，也是一个不错的模型。

半平面模型是一个在学习中广泛应用的模型，也是保角的，使用了整个上半平面作为映射，是笛卡尔盘模型的一个反演。

点击这里可以看到更多的在游戏中使用的模型。

#曲率半径

我们接下来讲一些更加与欧几里得几何不一样的特性。首先，在微分几何里，一个曲面是弯的还是平的的重要特征是，其上的一个方向向量，在沿着一个闭曲线平移一周之后，回来的方向与初始的方向不同。这就是曲率的体现。在游戏里则表现为，你绕了一个圈回来之后，整个视角的方向会旋转。双曲平面作为一个负常曲率空间，在这上面绕一圈之后，角度旋转的方向和绕的圈所包围的面积成正比。

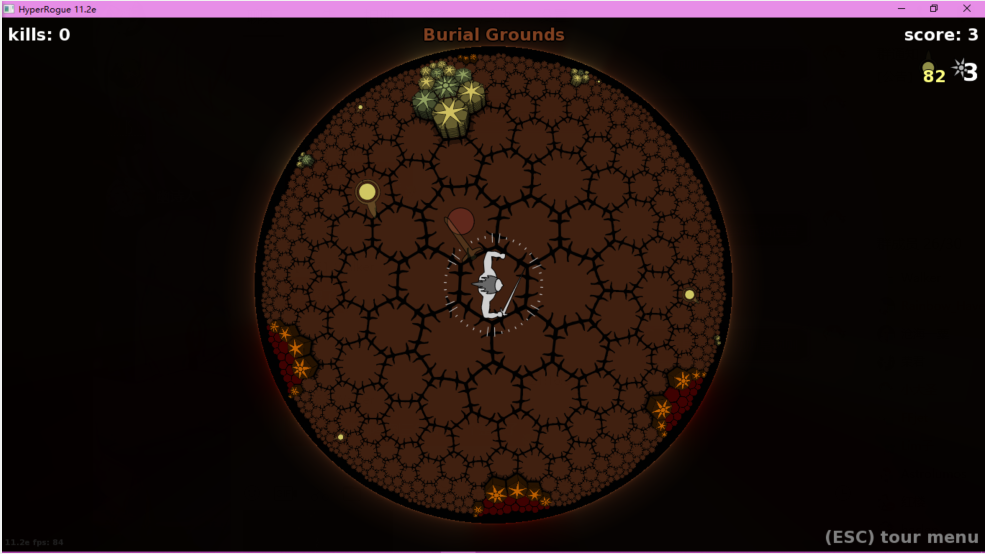
在游戏中，有这样一个大陆Burial ground，这个大陆里的武器只有一个一直指向固定方向的剑，你需要靠上面所述的性质，绕圈来改变剑的方向才能击杀敌人。

事实上，罗氏几何的多边形外角和大于\(2\pi\)（与欧几里得几何的严格等于\(2\pi\)不同），与上面说的曲率类似，外角和与\(2\pi\)的差值也和多边形的面积成正比。这也造成了罗氏几何里的一个特殊的情况：可以用角角角来判定三角形全等！

#有着重要地位的曲线——圆、等距圆与极限圆

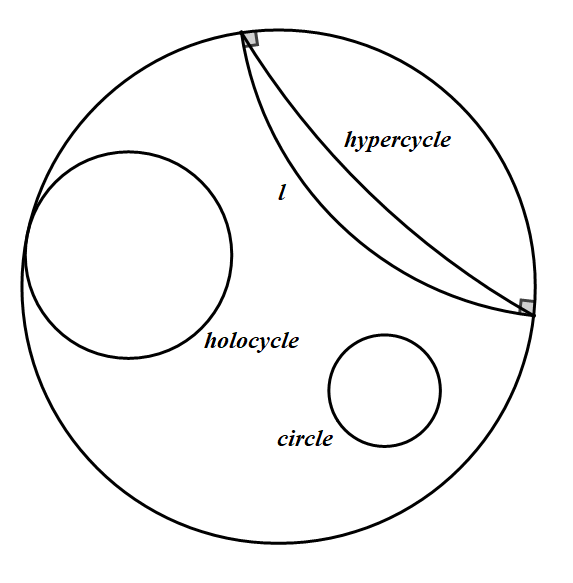
欧几里得几何里的圆有着特殊的地位。在罗氏几何里，有这样几种重要的曲线：圆、等距圆和极限圆。圆与欧几里得几何里的圆类似，定义为到一点距离相等的点的曲线，在笛卡尔盘模型里同样也是一个圆，但是其圆心可能会和欧几里得几何里的圆心完全不一样。由于两条平行线之间的距离不再是一直相等，可以做出这样的曲线叫等距圆，或者叫超圆（Hypercycle），是到一条直线距离相等的曲线。等距圆在笛卡尔盘模型里是一条不与边界圆垂直的圆弧。

在游戏里有这样一个大陆Land of eternal motion，这个大陆的陆地踩一下就会掉下去，你只能无限的往前走，也没有多余的回合去打怪物。但是即使是沿着直线向前走，也可以甩掉跟在自己侧后方的怪物，因为怪物实际上走的曲线是等距圆，而不是会和你分散的直线。在欧几里得几何里，跟在你后方的怪物你是永远也甩不掉的。

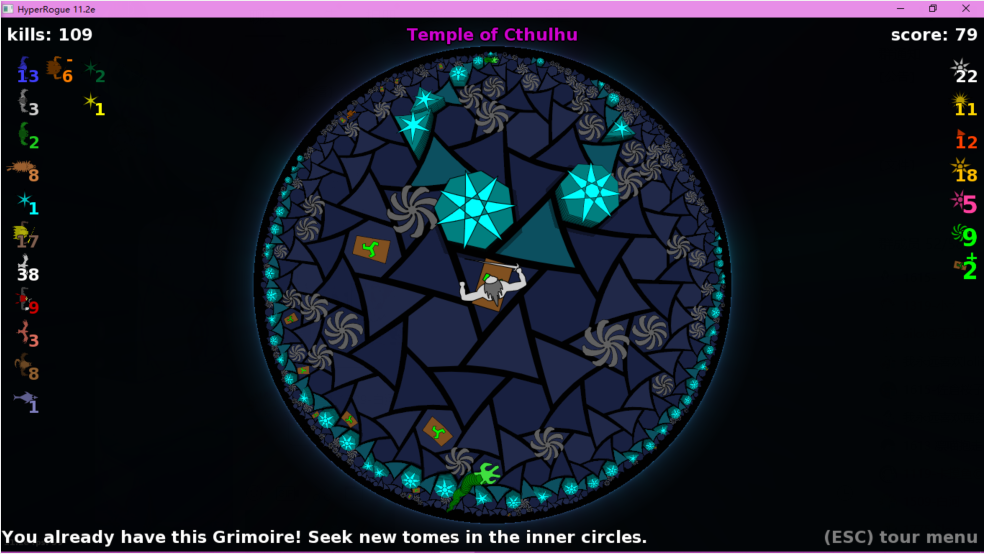
极限圆，或者叫浑圆（holocycle）定义为一组平行线组成的线束上的对应点的曲线，或者说垂直于这组平行线束的曲线。极限圆可以理解为圆在圆心趋向无穷远下的极限。极限圆在笛卡尔盘模型里是一个与边界圆内切的圆形。在游戏里，R'Lyeh里会有一个大陆Temple of Cthulhu（克苏鲁神殿），这个大陆是由无限嵌套的等距圆组成的，在每一层神殿里你只能拿一个宝石，想要获取更多的宝石就只能向神殿的无限深处前进。

过任何三点，能做且只能做直线、圆、等距圆、极限圆中的一者。

#罗氏几何与欧氏几何的相容性，以及其后世影响

最后一节，让我们以罗巴切夫斯基的精妙工作结束：他证明了罗氏几何与欧氏几何的相容性。在前面并没有叙述到的罗氏空间几何里，有一个曲面叫极限球，它与上面说的极限圆很类似。极限球与平面的交线是该平面上的一个极限圆。在极限球面上同样可以建立一个曲面几何学，将极限圆认作曲面上的直线后，配合一些概念的定义，它满足前面所述的I至IV的所有公理。但是！极限球上的极限圆同样可以建立平行理论。罗巴切夫斯基发现，在极限球上，过“直线”（也就是极限圆）外一点，有且只有一条“直线”与其不相交。也就是说在罗氏几何里，罗巴切夫斯基发现了一套欧几里得几何的系统。这也就说明了，如果欧几里得几何的公理之间有矛盾，那么罗巴切夫斯基几何也有。 相反，上面所述的每个模型，都是在欧几里得几何里找到了一套完整罗氏几何的系统。配合上一些射影几何的公式，可以在两者之间建立一一对应。如果罗氏几何的公理之间有矛盾，则欧几里得几何也有。 这也就证明了，罗氏几何和欧氏几何是相容的。在欧氏几何内无法找到第五公设的证明，也就相当于证明了第五公设的不可证明性。

罗巴切夫斯基几何对后世的影响极大。罗氏几何看起来描述的是一个虚构的，和现实的欧几里得几何完全不一样的几何，但是这之后，黎曼在罗巴切夫斯基的基础上，研究了黎曼几何，也就是我们现在所说的微分几何。微分几何用微分的手段研究高维曲面以及其内在性质，虽然在其刚被发现时还没有引起什么轰动，但是在之后的20世纪初，爱因斯坦建立的广义相对论中，产生了极大的影响。广义相对论认为时间和空间是一个整体，并且引力是时空弯曲的结果。定量化描述这个弯曲，用到的就是微分几何。这说明，物理上的时空实际上并不是欧几里得的几何，欧几里得几何只是实际时空的近似。

非欧几何学在分析上也有很大的影响。无穷小分析、复分析的保角变换等等，都与非欧几何有着很深刻的联系。

所有这些，使得罗巴切夫斯基的发现可被列为俄罗斯和全世界在科学上最伟大的成就之一。