#第五章 对称性与守恒律

• 5.1 量子化的角动量
• 5.2 空间反射对称性与P宇称
  • 5.2.1 轨道角动量的P宇称
  • 5.2.2 基本粒子的P宇称
  • 5.2.3 强子的P宇称
  • 5.2.4 光子的P宇称
  • 5.2.5 角动量和P宇称守恒
  • 5.2.6 弱相互作用中P宇称破坏
• 5.3 C宇称与T宇称
• 5.4 CP破坏与CPT定理
• 5.5 同位旋与G宇称

对称性在物理研究中十分重要。例如如果我们看到这样一个函数图像：

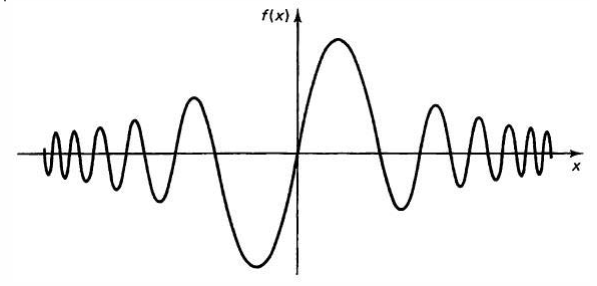
我们即使不知道它的函数表达式，但是只要知道它是奇函数，就能立即得到一系列性质，例如它在任意 区间内的积分都为0，它的泰勒展开中偶数次幂的系数都为0等等。在物理中，如果让我们求一个无限长直并且均匀带电的导线周围空间内的电场：

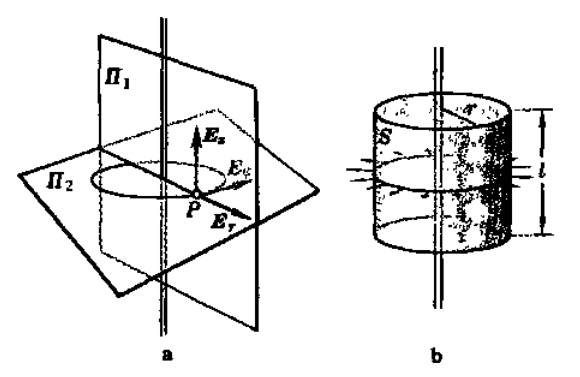
我们就可以首先依据对称性将问题进行简化。例如我们将研究问题在垂直方向上进行反射，空间内电荷分布保持不变，这说明在任意一点没有垂直方向上的电场；如果在水平方向上过导线的任意平面进行反射，同样保持不变，这说明在任意一点没有垂直于轴反向的电场；于是电场强度只能沿轴方向。又由于空间绕导线旋转之后，电荷分布也保持不变，这说明在任意不同的角度电场强度都相等；如果将空间沿垂直方向平移，电荷分布还是保持不变，这说明在不同高度电场强度也相等。我们仅仅通过对空间对称性的分析，就得到了在任意一点的电场方向，以及电场强度只是距离导线的距离 的函数这两个重要信息。这足以表明对称性分析在物理中的重要性。

在粒子物理的领域，同样有着诸多对称性。从空间和时间上的连续对称性来考虑，依据生活经验，我们可以知道，时空有一些连续对称性：空间平移对称性，空间旋转对称性，时间平移对称性。我们有诺特定理：每个连续对称性都有一个对应的守恒律。空间平移对称性生成动量守恒，时间平移对称性生成能量守恒，空间旋转对称性生成角动量守恒。全局的相位变换还可以生成量子数守恒，例如电荷守恒。

粒子物理当中，能量和动量守恒都和经典相对论物理类似，但是角动量的情况比较复杂，因为量子力学中角动量只能取分立值。我们先研究角动量。

#5.1 量子化的角动量

我们知道，在经典物理当中，角动量是 ，对于任何一个孤立系统来说，相对任意转动轴的角动量守恒。量子力学中，角动量被替换成了角动量算符，而角动量算符的本征值（也就是测量到的角动量数值）只能取分立值。具体来讲就是我们只能同时测得 和 ，而无法同时测量其x和y分量。对于一个 和 的本征态， 的本征值为 ， 的本征值为 ，其中 为一自然数， 为整数。而单个粒子也可能携带内禀的角动量，我们称为自旋 。对于 和 有类似的结果， 的本征值为 ， 的本征值为 ，但是区别是这里 可取半整数，。

即使在微观领域，角动量仍然必须守恒。但是粒子可能既有内禀角动量（自旋），也有轨道角动量（公转）。我们需要考虑角动量的合成。对于复合粒子例如 等的介子，就必须考虑两个夸克的自旋再加上夸克之间的轨道角动量，这三者之和。而重子则要考虑三个夸克的自旋和两部分轨道角动量，这五个量之和。

我们用 表示轨道角动量，总角动量 。对于一个系统，我们不可能同时确定 和 的全部分量。一种方法是我们单独考虑 和 ，选取 和 的本征态以及 和 的本征态，然后将它们相乘。例如：

我们也可以先测量总角动量 ，选取 和 的本征态，然后由于我们还差两个变量，可以再选取 和 ，这样也凑出来了四个变量：

后者可以让我们更直接的看出总角动量，而前者我们不一定能测量到确定的总角动量。所以我们更多的采取后面的来表示。这二者之间是可以换算的，一般的高等量子力学课程里面都会包括这部分计算，换算的系数叫 Clebsch–Gordan 系数，可以查表得到。例如对于 的情况（图里采用的符号是 ）：

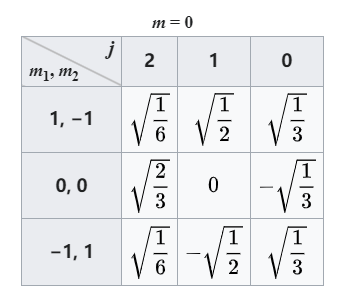
（注：这里写这个特殊情况当然是后面会用到）

如果我们采取 的共同本征态，那么轨道角动量 和自旋角动量 都有确定的取值。我们依照这个来分类粒子，将粒子表示为

的态的形式。中间的 我们一般不写数字，而是使用 等的符号，与氢原子能级较为类似。例如一个 的态会被表示为 态，一个 的态会被表示为 。

然后我们考虑介子。介子由一个夸克和一个反夸克组成，它们的自旋都是 。这时我们上面的 仍代表轨道角动量， 代表两个夸克的自旋之和。如果我们首先考虑轨道角动量为0的情况，这时 ，角动量就是两个 自旋的耦合。采用类似上述的方法，我们可以将 与 进行合成得到 ，得到 或 。也就是两个态：

而对于 ，我们则还要考虑刚刚耦合完的 继续与 耦合。 的情况，和 耦合会得到 ，而 时则会得到 的一组三重态。也就是四个态：

以 的举例的话，就是

我们可以看下面，粲偶素 与底偶素 的能谱，左面的六组态分别就是上面说的 态。由于粲夸克和底夸克较重，没有复杂的干涉叠加过程，我们单凭上面的简单夸克模型，就可以预测虚线之下的能谱。而这里有 等等则是轨道角动量相同也可能会有两者的环绕距离不同而导致有不同的能级，类似氢原子有 等的能级。最轻的两个粒子就是 态的两个粒子， 以及 ，它们的角动量分别为0和1。这里右上角的 和 马上会讲到。

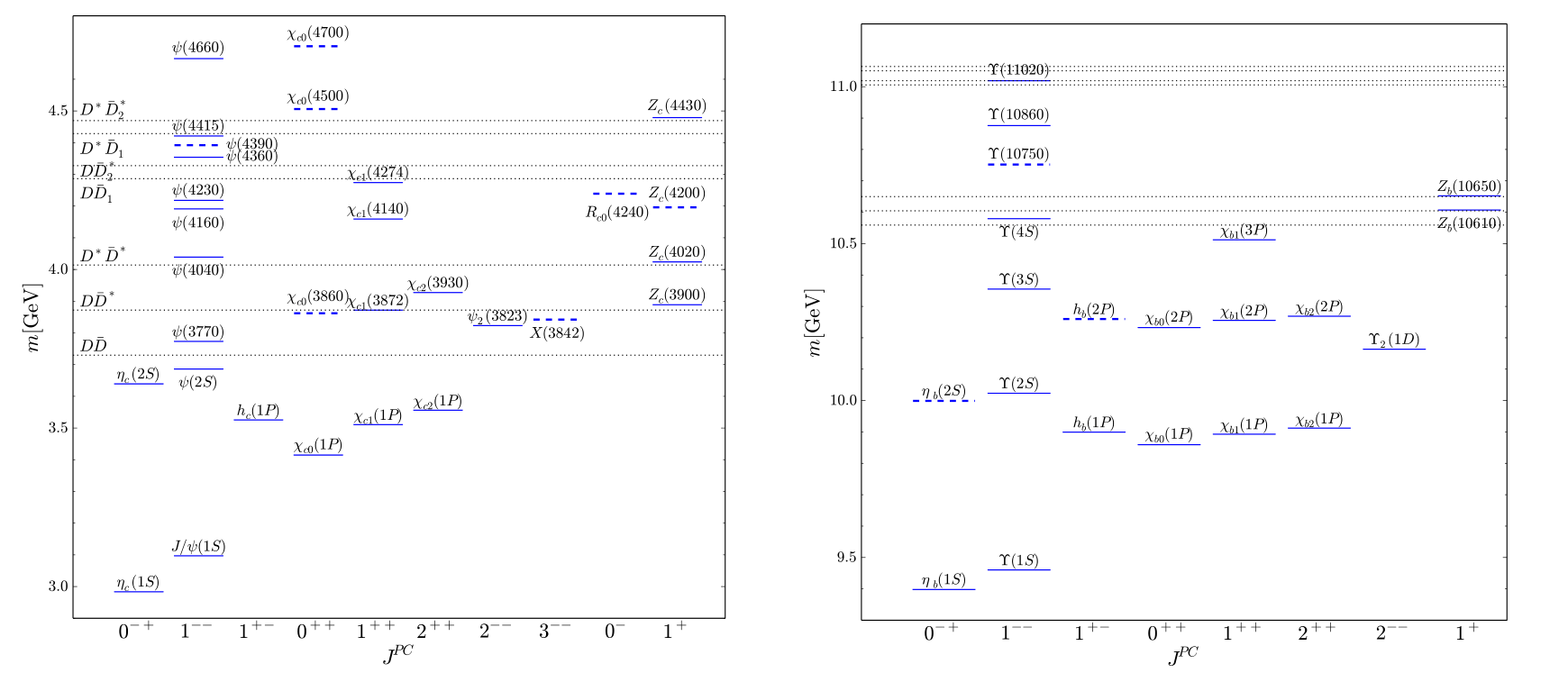
对于重子，重子含有三个夸克，它的 就是三个夸克的自旋之和。可能为 或 。而其轨道角动量则可以看成首先是两个夸克之间的轨道角动量 ，然后第三个夸克再绕这两个夸克运动的 ，之和。所以重子的可能态有：

可以看到重子谱会很复杂！但是当然，最轻的两种重子就是 或 。 等都是同一种夸克组分下自旋为 的最轻的态。

#5.2 空间反射对称性与P宇称

我们知道，空间不仅在平移旋转等连续变换下有对称性，还在反射下有对称性。我们无法区分我们的世界和镜子中的世界（当然我们马上就会看到其实是能区分的！）。

我们把空间反射变换定义为对一点反射，也就是 ，这样这个反射变换不依赖于反射的面。

即使在宏观，我们也会发现反射变换其实有可能存在一些问题。最典型的例子是磁感应强度。我们考虑一个电流环，根据右手定则可以确定电流环产生的磁场方向。但是我们如果在一个平行于电流环的镜子里观察电流环，电流方向应该不会变化，所以磁感应强度也不会反向。而如果电流环垂直于镜面，向下的磁感应强度在镜子里就变成了向上。这与我们一般理解的力或者电场在镜面反射下的变换完全不同。我们管这种矢量叫做轴矢量，或者赝矢量。与之相对，遵循力或是电场这种反射变换的矢量叫极矢量。轴矢量一般都是两个极矢量的叉乘，这导致了它们在对称性变换下的行为不同。这在对点反射的情况下也相同，在对点反射变换下，电场等极矢量会加一个负号，而磁场等轴矢量不会，仍然保持不变。

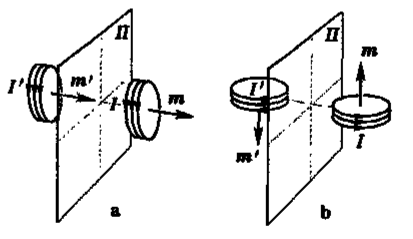
类似地，我们可以对其他量在空间反射变换下的反应分类。例如可以存在标量（在反射变换下不变）和赝标量（在反射变换下会增加一个负号的标量）。赝标量的一个例子是磁通量，也就是磁场强度这个赝矢量与面积矢量的点乘。

对于一个粒子，其波函数也可以被空间反射变换算符所作用。如果这个粒子是空间反射变换算符的本征态（大部分粒子都是，因为总不会期望一个粒子被反射之后就变成了另两个粒子的叠加态），那么由于粒子经过连续两次反射之后会变回自己，所以此本征值必然是正负1之一。我们可以通过一个粒子的P宇称为 或是 来归类粒子。

在一般过程中，P宇称是守恒的，这意味着反应前后两端的所有粒子以及轨道波函数的P宇称之积相等。也就是P宇称与之前所讨论的角动量、电荷等相加性守恒量不同，P宇称是相乘性守恒量。

#5.2.1 轨道角动量的P宇称

我们接下来考虑具体的P宇称的例子。首先，P宇称是空间变换，也就意味着粒子在空间中的运动，也就是轨道角动量，对P宇称也有贡献。轨道角动量的P宇称可以通过对球谐函数的计算得到，结果是：。也就是，S波的P宇称是 ，P波的P宇称是 ，D波的P宇称是 ，以此类推。也就是如果我们考虑两个P宇称分别为 和 的粒子组成的束缚态，其S波基态的轨道角动量为0，所以P宇称应该是 ，其第一个P波激发态的P宇称就是 ，等等。

#5.2.2 基本粒子的P宇称

然后我们来看基本粒子的P宇称。根据量子场论，电子和正电子的P宇称之积必须是 （这里不做证明）：

其他类似的自旋为 的费米子也一样。这一结果可以通过实验证明。实验上可以研究正负电子互相绕转组成的电子偶素的湮灭：

我们可以考虑电子偶素的基态，其轨道角动量 ，所以总的P宇称就是正负电子的P宇称之积 。由于末态是两个光子，末态的P宇称应该是 ，其中 是末态两个光子之间的轨道角动量，可以通过测量末态两个光子的极化得到。由于电磁相互作用里P宇称守恒，我们就可以推算出正负电子的P宇称之积。实验结果支持了其积是 的计算。

但是我们实际上无法确定单个电子本身的P宇称。我们能够测量的过程都是诸如 或是 的过程，因为单个电子无法被创造或是消失。我们只能约定单个电子的P宇称。目前通用的约定是电子、 子、 子的P宇称都是 ，其反粒子的P宇称都是 。也就是：

然后我们可以得到

对于夸克来讲，情况是类似的。我们无法在强相互作用和电磁相互作用中单独产生夸克。所以我们同样规定夸克的P宇称都是 ，反夸克的P宇称都是 ：

于是

#5.2.3 强子的P宇称

这样，我们就可以继续计算由夸克组成的复合粒子，也就是介子和重子的P宇称。介子 的P宇称就是：

也就是介子的P宇称与轨道角动量关联，轨道角动量为偶数的介子P宇称为负，轨道角动量为奇数的介子P宇称为正。这时我们可以回来看粲偶素和底偶素的能谱，最低的两个态都是S波态，其P宇称都是负；右侧的四个态都是P波态，其P宇称都是正。

而对于重子， 的P宇称就是：

而反重子的P宇称就是 。对于最低能量的态，，我们就可以预测出最低能量的态的P宇称均为正。事实上 的P宇称都是正的。

上面我们是通过规定了六种夸克的P宇称来确定所有强子的P宇称的。事实上，我们也可以通过规定几种强子的P宇称来确定其余强子的P宇称，这样做的好处是它可以直接与实验相联系，夸克在实验上无法直接创造，而其余的强子可以。例如我们可以规定 ，这样就可以定下 和 夸克的P宇称。对于其余几种夸克，我们可以规定 ，这样与之前规定所有夸克的P宇称都是 是等价的。

#5.2.4 光子的P宇称

光子的P宇称我们可以直接通过麦克斯韦方程组得到。例如，电场应满足高斯方程：

由于在空间反射变换下 保持不变，，而 变号，故 在反射作用下应变号：。而由于

由于我们考虑光子，空间中没有静电荷，故可以令 ，那么在空间反射变换下 就应当变号：。在量子场论下，描述光子波函数的实际上就是矢量势 ，故我们得到光子的P宇称是 。

#5.2.5 角动量和P宇称守恒

在强相互作用和电磁相互作用下，角动量和P宇称都是守恒的。实际上我们也经常将这二者一起考虑，描述粒子属性时也经常将它们结合在一起，表示为自旋宇称 。下面我们举几个例子说明一下。

我们看一个激发态 介子衰变到一个 介子和一个 介子的过程。这是一个强或电磁衰变。每个粒子的自旋宇称也都写在了上面。衰变左侧的角动量是1，而右侧的角动量是0+0再加轨道角动量，它等于1。这说明轨道角动量只能是1，也就是这个衰变是一个P波衰变。然后看宇称，左侧的宇称为负，右侧的宇称是负乘以负乘以 也就是负。两侧宇称守恒。那么如果是衰变到 呢？光子的自旋宇称是 ，等式右侧的角动量是 轨道角动量等于1，说明轨道角动量可以取0,1,2。而根据宇称守恒，右侧的轨道角动量只能是奇数，所以这说明这个衰变也是一个P波衰变。再看一个例子

左侧的角动量是0，右侧的角动量是0+0加轨道角动量，说明轨道角动量只能是0。然后看宇称，左侧的宇称为负，右侧的宇称是负乘以负乘以 是正，两侧宇称不相等，说明这个反应不可能作为强相互作用或者电磁相互作用发生。实验上也确实没有观测到这个衰变，分支比的上限为 。

#5.2.6 弱相互作用中P宇称破坏

历史上，科学家们曾经发现过两个粒子 和 ，它们有完全相同的质量、电荷、寿命、自旋（都为0），但是一个衰变为2个 ，一个衰变为3个 ：

但是它们的P宇称不一样。这使得杨振宁和李政道去寻找了之前关于弱相互作用中P宇称是否守恒的实验证据。他们发现之前完全没有弱相互作用中P宇称守恒的证据，于是吴健雄做了一个实验，观察极化的钴-60衰变放出的电子的方向。结果他们发现，弱相互作用中P宇称并不是守恒的。所以实际上 和 就是同一个粒子，现在叫 介子。

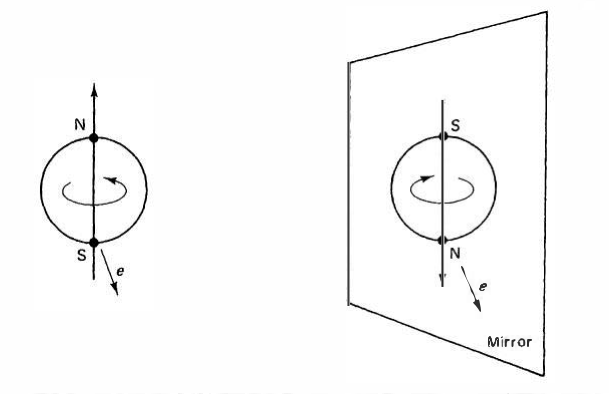
实际上我们之后可以看到，弱相互作用中P宇称实际上是最大地被破坏了的。为理解这点，我们考虑一束沿着运动方向自旋的粒子，比如，它可以是沿运动方向的右手方向自旋，也可以是左手方向自旋，我们管这两部分叫做右旋电子和左旋电子。我们考虑一束右旋电子，如果我们在比电子飞行速度更快速的参考系里看这束电子的话，那么这束电子就会变成向后飞的，也就是从右旋变成了左旋。

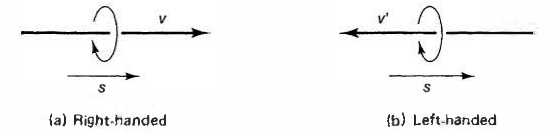
但是如果这并不是电子，比如是无质量的中微子，它以光速运动，我们不可能比它更快；这就意味着右旋的中微子将永远保持右旋，左旋的中微子也将永远保持左旋，我们将无法看到这两部分的相互转化。那么我们就可以在实验里寻找左旋和右旋中微子，看看它们占比多少。以前人们曾认为，这两部分应该是一半一半的。但是实际情况却是，所有的中微子都是左旋的，所有的反中微子都是右旋的。这也某种程度表明了弱相互作用中宇称的破坏程度之大。

注：当然现在我们知道中微子的质量虽然很小很小，但是不是0，这使得右旋中微子和左旋反中微子又有可能存在了。但是之所以我们没有观测到它们有可能是因为一些奇奇怪怪的机制，这里就不过多地讲了。

#5.3 C宇称与T宇称

电荷共轭变换，也叫C变换是将粒子变成反粒子、反粒子变成粒子的变换。如果一个粒子的反粒子就是其自身，或者由一对正反粒子组成，例如 由 或 组成，那么C变换会将粒子变为自身。我们可以类似P宇称的定义，考虑C变换算符作用在粒子波函数的本征值，称为C宇称。由于连续进行两次C变换必定将粒子变为自身，故C宇称的值也为 。

例如 的C宇称，C算符会把 变成 ，把 变成 ，所以在经过C算符的变换下， 的两个夸克相当于互换了位置。那么这就和P宇称类似了。量子场论的计算得出，一对正反费米子 的C宇称等于其轨道角动量加上自旋角动量 。我们也可以观察粲偶素的能谱来得到这一点。

光子的反粒子为其自身，对于光子的C宇称，我们同样可以直接计算得到。在C变换下，空间位置不变，但是电荷量应当变号。故 ，。所以 也应当变号，说明光子的C宇称为 。

在实验上，强相互作用和电磁相互作用保持C宇称不变。一个典型的例子是 。首先由于 是一个 态，其C宇称为 。衰变到两个光子，两个光子的C宇称之积为 。而 我们也可以画出其费曼图，有可能作为电磁相互作用发生，但是实际上其左侧C宇称为 ，右侧C宇称为 ，两侧C宇称不守恒，故此衰变不可能发生。实验上也确实没有观测到其发生，衰变分支比的上限是 。

#5.4 CP破坏与CPT定理

#5.5 同位旋与G宇称