抛物线规作图2

在之前，我们研究过抛物线规作图，链接

那里提到，从两点(0,0)和(1,0)开始，抛物线规强于尺规，不仅可以做加减乘除开方还能够解最多四次的方程。但是从三点开始，目前没有解决已知(0,0)(1,0)(a,b)求作(a,0)的问题。现在这个问题被 xurui 解决了。作图如下：

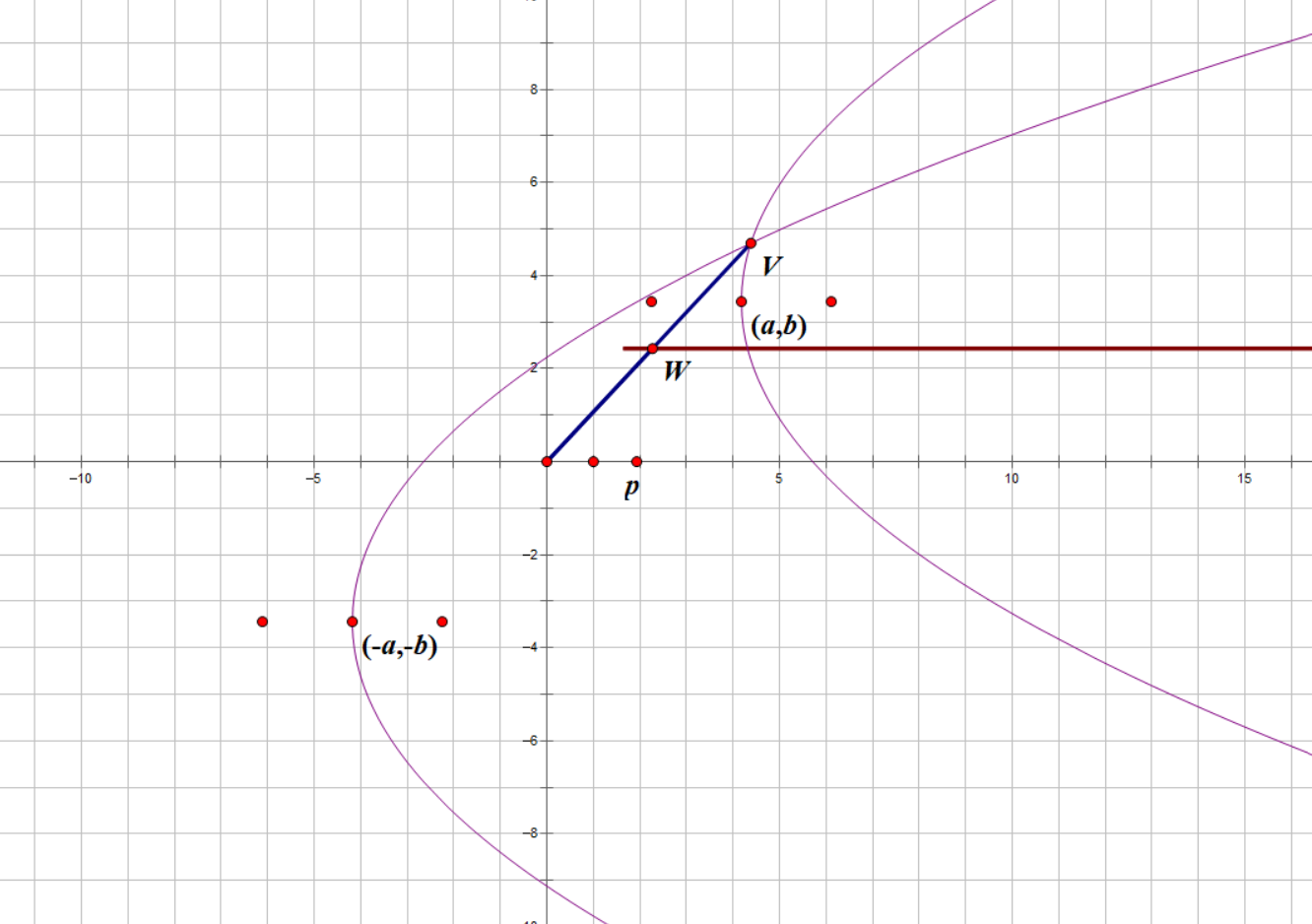
尝试计算以(a,b)为顶点和(-a,-b)为顶点，开口方向与大小都相同的抛物线（例如）的交点。联立和可以解出交点为。如果是的话，得到的交点为。将后者的xy坐标乘以2与前者相减即可得到。这样就可以提取出(a,b)的y坐标了。由此我们得出一下作图法：

作图 1. 已知三点A、B与C，可作C在直线AB上的投影（或者说垂足）M。
不妨设A(0,0)，B(1,0)，C(a,b)。首先仅用(0,0)和(a,b)两点，使用之前的方法，作出(-a,-b)。然后仅用(0,0)和(1,0)两点，作出和。然后以(0,0) 作平行四边形得到和。对这两对点做抛物线，作出两条以(a,b)和(-a,-b)为顶点的抛物线。这两条抛物线交于P点。以相同方法，将换成作出两个抛物线的交点Q点。
根据上述计算，直线PQ与直线AB垂直。作平行四边形APQR，R点坐标即为。将R点转移至x轴上，除以3并开根号即可得到M点。

在已知(0,0)和(1,0)之后，用上述方法可以将任何给出的点的横纵坐标提取出来。然后再利用之前的作图法，可以作出所有四则运算开根号或是解四次方程。

至此，抛物线规作图已全部完成。抛物线规不仅能代替尺规，作出直线或是圆的交点，还可以倍立方或是三等分任意角，甚至解四次方程。由于抛物线为二次曲线，相交最多只能是四次方程，所以这也就是抛物线规全部的潜力了。